一、面板数据回归分析的Stata实现

   作为功能全面、操作简明的统计分析工具，Stata在数据处理与模型估计方面具有显著优势。其系统整合了数据管理、统计分析与图形展示等功能，尤其擅长处理面板数据、时间序列数据及复杂调查数据。对于会计学领域的研究而言，面板数据因其能够同时反映个体与时间维度的变化而得到广泛使用。因此，熟练掌握Stata中面板数据的回归操作方法，具有重要的学术价值与实践意义。

   本文旨在介绍基于Stata进行面板数据回归分析的主要步骤与相关命令。具体内容涵盖模型设定、估计方法选择以及结果解释等方面，为相关研究提供技术参考。

二、面板数据的基本概念

   面板数据，亦称纵列数据或追踪数据，是计量经济学与统计学研究中一种重要的数据结构。它是指在时间维度上对一组固定个体进行重复观测所获得的数据集合，本质上是截面数据与时间序列数据的有机结合。

   具体而言，面板数据包含两个维度：截面维度（通常为不同的个体，如地区、机构或家庭）与时间维度（连续的观测时期）。例如，在研究省级经济发展时，若对31个省级行政区连续观测38年（如1979年至2016年），便可得到一个包含1178个观测值的平衡面板数据集。这种数据结构能够同时反映个体间的差异与个体随时间的变化趋势，为控制不可观测的个体异质性提供了可能，因而在实证研究中具有显著优势。

三、面板数据模型的优势 

   面板数据模型在计量经济分析中具有若干显著优势，主要体现在以下几个方面：

   首先，该模型能够有效控制不可观测的个体异质性与时间效应。在实证研究中，常存在诸如地区文化、个体偏好或特定时期冲击等难以量化或观测的因素。若忽略这些因素，可能导致遗漏变量偏误。面板数据模型通过引入个体固定效应或时间固定效应，能够在估计过程中控制这些不随时间变化或不在个体间变化的特征，从而提升参数估计的一致性。

   其次，面板数据结构包含更多信息与变异。由于同时结合了截面与时间两个维度，其观测值数量通常显著增加，这不仅提高了估计的自由度，也能减弱解释变量间可能存在的多重共线性问题，从而提升估计效率与统计推断的可靠性。

   最后，面板数据模型特别适用于分析经济行为的动态调整过程。例如，个体的当期决策常受到过去行为的影响，面板数据允许研究者将滞后因变量纳入模型，从而更准确地刻画和检验这种动态依赖关系。

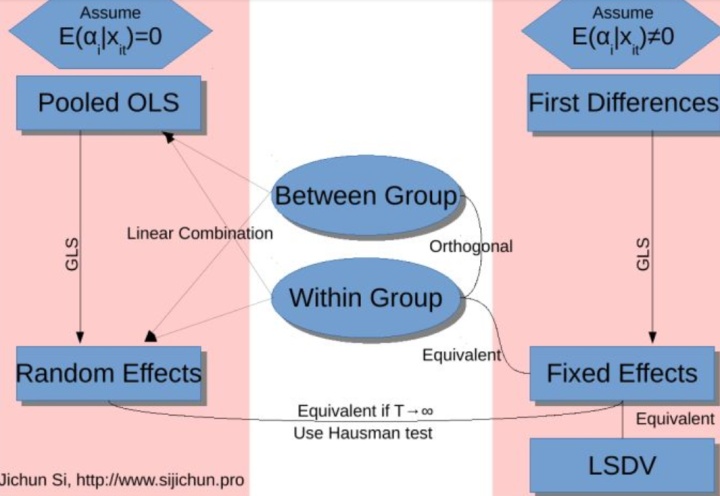
四、面板模型的选择：固定效应与随机效应

   在面板数据分析中，处理不可观测的个体效应主要存在两种方法，由此衍生出两种基本模型：固定效应模型与随机效应模型。二者核心区别在于对个体效应性质的设定不同。

   固定效应模型将个体差异视为待估参数，表现为每个个体拥有独特的截距项。该模型允许个体效应与模型中的解释变量存在任意相关性，其估计目标在于分析样本内个体自身的动态变化。相比之下，随机效应模型则将个体差异视为来自某一总体的随机变量，并纳入复合误差项。该模型假定个体效应与所有解释变量均不相关，其估计目标在于对总体特征进行推断。

   关于模型选择，一种观点依据研究样本与母体的关系。若样本近乎构成研究对象的全部（如对中国全部省级行政区的研究），个体效应可视为固定参数，宜采用固定效应模型。若样本仅为大母体中的一个随机子集（如对某城市数千名居民的抽样调查），则更适用随机效应模型。

   然而，更严谨的模型选择应基于计量经济学假设的检验。随机效应模型的有效性依赖于“个体效应与解释变量不相关”的关键假设。若该假设成立，随机效应估计量比固定效应估计量更为有效；若该假设不成立，则随机效应估计量将产生不一致的估计结果，此时应使用固定效应模型。

   为检验这一关键假设，Hausman检验是常用的判别方法。其原假设为个体效应与解释变量无关（即随机效应模型假设成立）。检验通过比较固定效应与随机效应估计量的一致性差异构建统计量。若检验拒绝原假设，则表明个体效应与解释变量存在相关性，应选择固定效应模型；若无法拒绝原假设，则表明随机效应模型的假设得到支持，采用随机效应模型可以获得更有效的估计结果。

五、Stata面板数据回归操作流程

   以下将系统介绍在Stata软件中进行面板数据回归分析的标准步骤，涵盖数据准备、模型设定、估计检验及结果解读等环节。

（一）数据导入与准备
   在导入数据前，建议对原始数据进行预处理。对于外部数据文件，可使用标准导入命令进行加载；若需从其他软件或格式转入，可通过数据编辑器进行转换。为确保分析顺利进行，变量名称应使用英文标识，避免包含中文字符，同时应妥善处理数据中的缺失值。变量重命名命令可用于建立清晰的分析变量体系。

（二）设定面板数据结构
   进行面板数据分析前，必须明确定义数据的面板结构特征。通过指定截面标识变量和时间标识变量，可将数据格式正式声明为面板数据。该步骤是后续所有面板数据分析命令运行的基础前提。

（三）模型估计方法
   面板数据回归主要提供三种估计方法选择：

  ✔️混合最小二乘法：假设所有个体具有相同的截距项，忽略个体间的异质性特征。

  ✔️固定效应模型：通过组内变换消除不随时间变化的个体特征，适用于个体效应与解释变量存在相关性的情况。

  ✔️随机效应模型：假设个体效应与解释变量不存在相关性，采用广义最小二乘法进行参数估计。

（四）模型选择检验
   在固定效应模型与随机效应模型之间进行选择时，需要借助统计检验。Hausman检验通过比较两种模型的估计结果是否存在系统性差异，为模型选择提供依据。检验的原假设支持随机效应模型。若检验结果显著，表明个体效应与解释变量存在相关性，应选择固定效应模型；若不显著，则支持随机效应模型。

   当检验统计量出现异常值时，可能表明模型设定存在问题，需重新审视模型的基本假设条件。

（五）结果解读与报告
   模型估计完成后，应系统分析估计结果。需重点关注解释变量的系数方向、幅度及其统计显著性，同时考察模型的整体拟合效果。对于固定效应模型，主要关注组内拟合优度；随机效应模型则需要同时考虑组内、组间和总体拟合程度。最后，应结合具体研究背景，对实证结果的经济学或管理学含义进行合理解释。

   通过遵循上述规范化操作流程，研究者能够系统完成面板数据回归分析，确保研究过程的严谨性与研究结论的可靠性。

乐备实（上海优宁维生物科技股份有限公司旗下全资子公司），是国内专注于提供高质量蛋白检测以及组学分析服务的实验服务专家，自2018年成立以来，乐备实不断寻求突破，公司的服务技术平台已扩展到单细胞测序、空间多组学、流式检测、超敏电化学发光、Luminex多因子检测、抗体芯片、PCR Array、ELISA、Elispot、PLA蛋白互作、多色免疫组化、DSP空间多组学等30多个，建立起了一套涵盖基因、蛋白、细胞以及组织水平实验的完整检测体系。

 
我们可提供从样本运输、储存管理、样本制备、样本检测到检测数据分析的全流程服务。凭借严格的实验室管理流程、标准化实验室操作、原始数据储存体系以及实验项目管理系统，已经为超过3000家客户单位提供服务，年检测样本超过100万，受到了广大客户的信任与支持。